AI techniques like large language models (LLMs) are rapidly transforming many scientific disciplines. Quantum computing is no exception. A collaboration between NVIDIA, the University of Toronto, and Saint Jude Children’s Research Hospital is bringing generative pre-trained transformers (GPTs) to the design of new quantum algorithms, including the Generative Quantum Eigensolver (GQE) technique.
The GQE technique is the latest in a wave of so-called AI for Quantum techniques. Developed with the NVIDIA CUDA-Q platform, GQE is the first method enabling you to use your own GPT model for creating complex quantum circuits.
The CUDA-Q platform has been instrumental in developing GQE. Training and using GPT models in quantum computing requires hybrid access to CPUs, GPUs, and QPUs. The CUDA-Q focus on accelerated quantum supercomputing makes it a fully hybrid computing environment perfectly suited for GQE.
According to GQE co-author Alan Aspuru-Guzik, these abilities position CUDA-Q as a scalable standard.
Learning the grammar of quantum circuits
Conventional LLMs can be a useful analogy for understanding GQE. In general, the goal of an LLM is to take a vocabulary of many words; train a transformer model with text samples to understand things like meaning, context, and grammar; and then sample the trained model to produce words, which are then strung together to generate a new document.
Where LLMs deal with words, GQE deals with quantum circuit operations. GQE takes a pool of unitary operations (vocabulary) and trains a transformer model to generate a sequence of indices corresponding to unitary operations (words) that define a resulting quantum circuit (document). The grammar for generating these indices is a set of rules trained by minimizing a cost function, which is evaluated by computing expectation values using previously generated circuits.
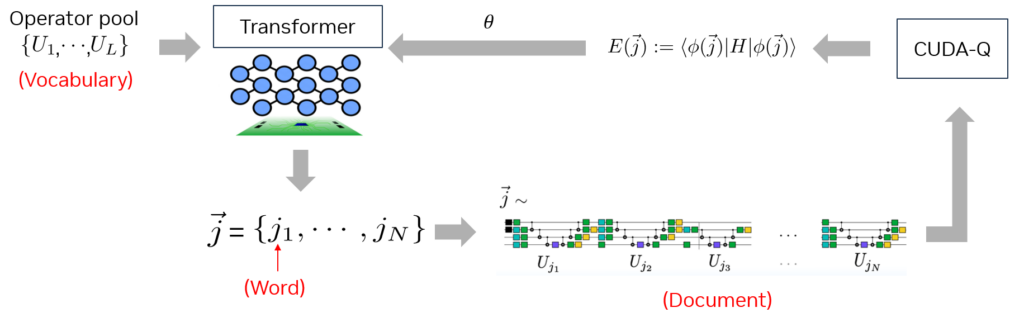
Figure 1 shows that GQE is analogous to a LLM. Instead of adding individual words to construct a sentence, unitary operations are added to generate a quantum circuit.
GQE-enabled algorithms.
In the era of noisy, small-scale quantum (NISQ) computers, quantum algorithms are limited by several hardware constraints. This has motivated the development of hybrid quantum-classical algorithms like the Variational Quantum Eigensolver (VQE), which attempts to circumvent these limitations by offloading onerous tasks to a conventional computer.
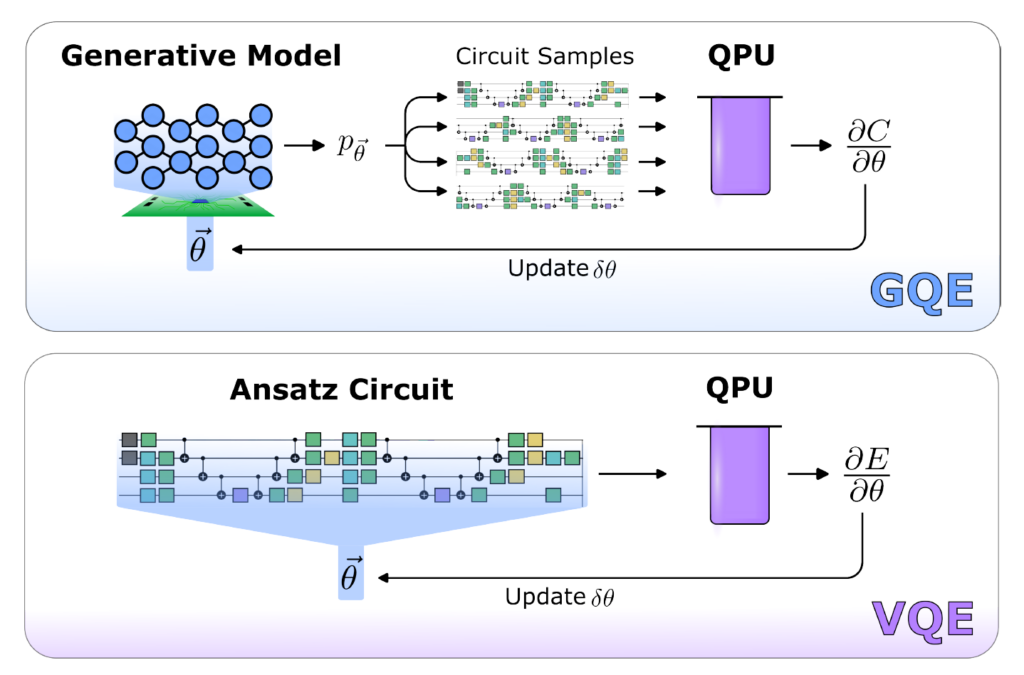
All optimized parameters are handled classically in the GPT model and are updated based on the expected values of the generated circuits. This enables optimization to occur in a more favorable deep neural network landscape and offers a potential route to avoiding the barren plateaus that impede variational algorithms. This also eliminates the need for the many intermediate circuit evaluations required in techniques like reinforcement learning.
The GQE method is the first hybrid quantum-classical algorithm leveraging the power of AI to accelerate NISQ applications. GQE extends NISQ algorithms in several ways:
- Ease of optimization: GQE builds quantum circuits without quantum variational parameters (Figure 2).
- Quantum resource efficiency: By replacing quantum gradient evaluation with sampling and backpropagation, GQE is expected to provide greater utility with fewer quantum circuit evaluations.
- Customizability: The GQE is very flexible and can be modified to incorporate a priori domain knowledge, or applied to target applications outside of chemistry.
- Pretrainability: The GQE transformer can be pretrained, eliminating the need for additional quantum circuit evaluations. We discuss this later in this post.
Results from GPT-QE
For the inaugural application of GQE, the authors built a specific model inspired by GPT-2 (referred to explicitly as GPT-QE) and used it to estimate the ground state energies of a set of small molecules.
The operator pool of vocabulary was built from chemically inspired operations such as excitations and time evolution steps that were derived from a standard ansatz known as ‘unitary coupled-clusters with single and double excitations’ (UCCSD). An ansatz is an approach to parameterizing quantum circuits.
Variational algorithms must be started with a ‘best guess’ initial state, generated with existing classical methods. To demonstrate GPT-QE, the authors generated an initial state using the Hartree-Fock method with an STO-3G basis set. The GPT model used in this work was identical to OpenAI’s GPT-2 model, including 12 attention layers, 12 attention heads, and 768 embedding dimensions. For more information and a comprehensive technical explanation of the training process, see 2.2. GPT Quantum Eigensolver in The generative quantum eigensolver (GQE) and its application for ground state search.
A great advantage of this technique is that it is highly parallelizable, both in terms of using GPU acceleration for the classical component and in using multiple QPUs for the quantum calculations. Since the publication of the paper, the workflow has been accelerated by parallelizing the expectation value computations of the GPT-QE sampled circuits using the NVIDIA CUDA-Q multi-QPU backend, mqpu.
The mqpu backend is designed for parallel and asynchronous quantum co-processing, enabling multiple GPUs to simulate multiple QPUs. As the availability of physical quantum hardware increases, these backends can trivially be replaced with access to multiple instances of potentially varying QPU hardware.
Figure 3 shows the speedup realized by using the nvidia-mqpu backend on a much larger 18-qubit CO2 GQE experiment. Baseline CPU computations were obtained by calculating the expectation value of 48 sampled circuits on a 56-core Intel Xeon Platinum 8480CL E5.
Using a single NVIDIA H100 GPU instead of the CPU provided a 40x speedup. The CUDA-Q mqpu backend provides an additional 8x speedup by enabling asynchronous computation of the expectation values across eight GPUs using an NVIDIA DGX-H100 system.
The authors also trained a 30-qubit CO2 GQE experiment for which the CPU failed. The model trained in 173 hours on a single NVIDIA H100 GPU, which was reduced to 3.5 hours when parallelized across 48 H100 GPUs.
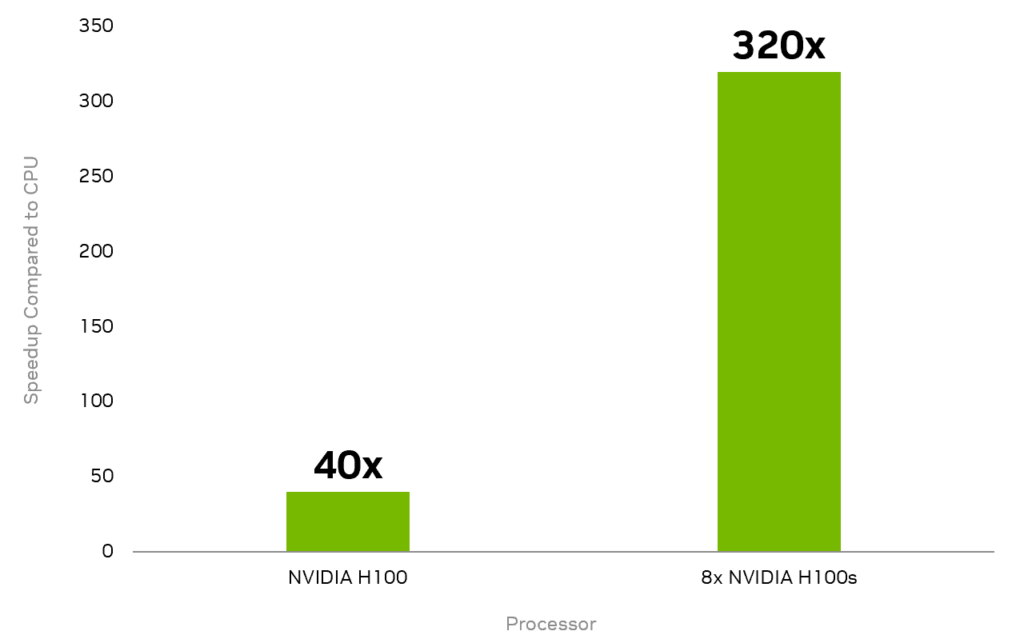
Figure 3 shows GQE circuit samples accelerated with a single NVIDIA H100 GPU or asynchronous evaluation across multiple GPUs using an NVIDIA DGX-H100.
As the scale of quantum computations continues to increase, the ability to parallelize simulation workloads across multiple GPUs, and eventually QPUs, will become increasingly important.
Beyond access to these hardware capabilities, implementing GPT-QE using CUDA-Q provided additional benefits like interoperability with GPU-accelerated libraries such as PyTorch to accelerate the classical parts of the algorithm. This is a huge benefit of the CUDA-Q platform, which also has access to the world’s fastest implementations of conventional mathematical operations through the GPU-accelerated CUDA-X libraries.
The CUDA-Q QPU agnosticism is also key in enabling future experiments on multiple physical QPUs. Most importantly, by embodying hybrid quantum computing and offloading gradient calculations to classical processors, large-scale systems can be explored and open the door to useful quantum computing applications enabled by AI.
Opportunities to extend the GQE framework
This collaboration is a first step towards understanding the broad opportunities for how GPT models can enable quantum supercomputing applications.
Future research will hone exploring different operator pools for GQE and optimal strategies for training. This includes a focus on pretraining, a process where existing datasets can be used to either make the transformer training more efficient or aid in the convergence of the training process. This is possible if there is a sufficiently large data set available containing generated circuits and their associated expectation values. Pretrained models can also provide a warm start for training other similar models.
For example, the output from a prior run would create a database of circuits and their associated ground state energies. Poorly performing circuits can be thrown away and the transformer can be trained using only the better-performing circuits, without the need for a quantum computer or simulator. This pretrained transformer can then be used as the initialization point for further training, which is expected to converge quicker and exhibit better performance.
There is also a huge scope for applications using GQE outside of quantum chemistry. A collaboration between NVIDIA and Los Alamos National Lab is exploring using the ideas of GQE for geometric quantum machine learning.
For more information about the GQE code, including examples, see the GQE GitHub repo.
The GQE is a novel example of how GPT models and AI in general can be used to enable many aspects of quantum computing.
NVIDIA is developing hardware and software tools such as CUDA-Q to ensure scalability and acceleration of both the classical and quantum parts of hybrid workflows. For more information about NVIDIA’s quantum efforts, visit the Quantum Computing page.